Y=x^2 2 644031-Y x 2 2 m-1 x 3-m 2
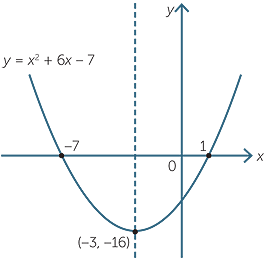
What Is The Vertex Of Y X 2 6 Socratic
2y) x2 (x2y) p x2y = y (x y)3= @2f @y 2 = 1 2 @f @y (p x2y) = 2 0 p x2y p1 1 2 x2y (x y) = 1 4 x 2y)3= 3 Serie bis Mo, 2 5 11 ;1 Anhand der De nition Wir wissen f( x u) f( x) = Df( x)u o(u) 2 Ist u= tv;t2IR;v2IR2;v6= 0, so
Y x 2 2 m-1 x 3-m 2
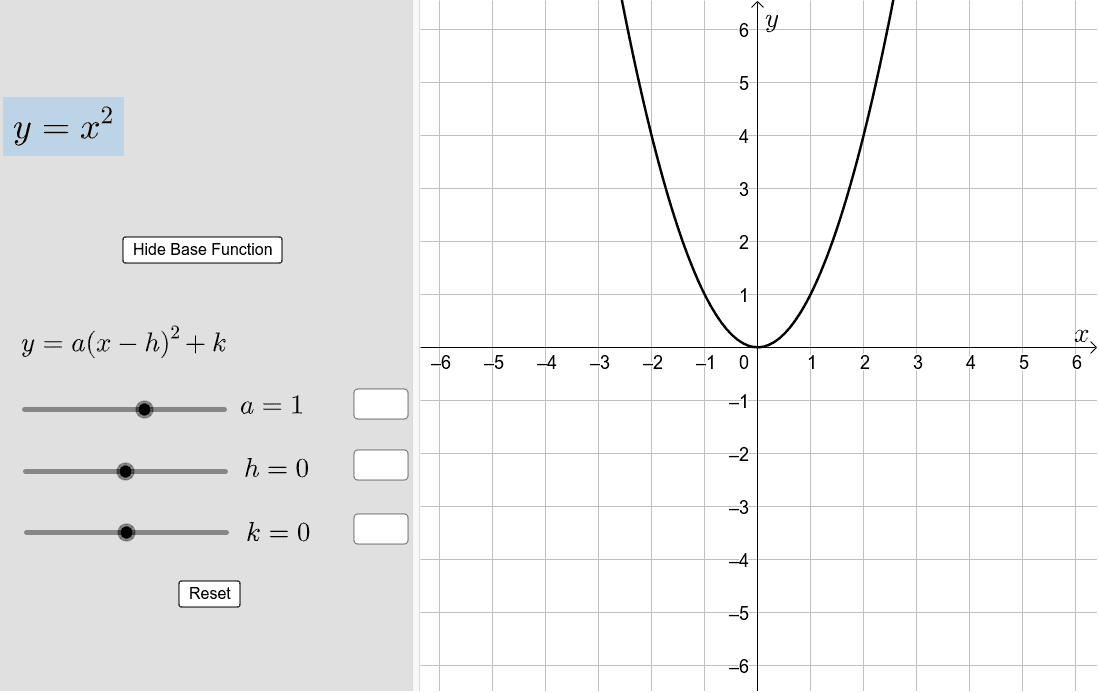
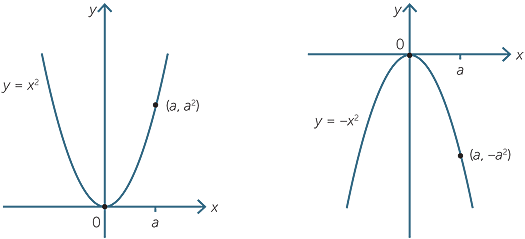
Y x 2 2 m-1 x 3-m 2-Y = k − p y = k p Substitute the known values of p p and k k into the formula and simplify y = − 9 4 y = 9 4 y = − 9 4 y = 9 4 Use the properties of the parabola to analyze and graph the parabola Direction Opens Up Vertex ( 0, − 2) ( 0, 2) Focus ( 0, − 7 4) ( 0, 7 4) Axis of Symmetry x = 0 x = 0Set y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down
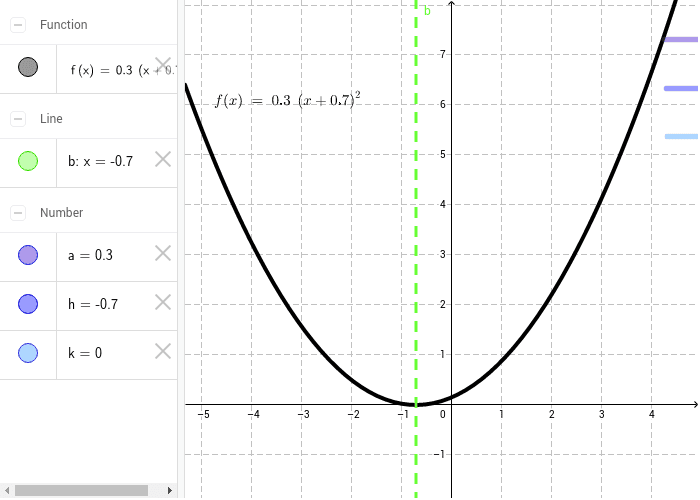
Transformations To The Graph Of Y X 2 Geogebra
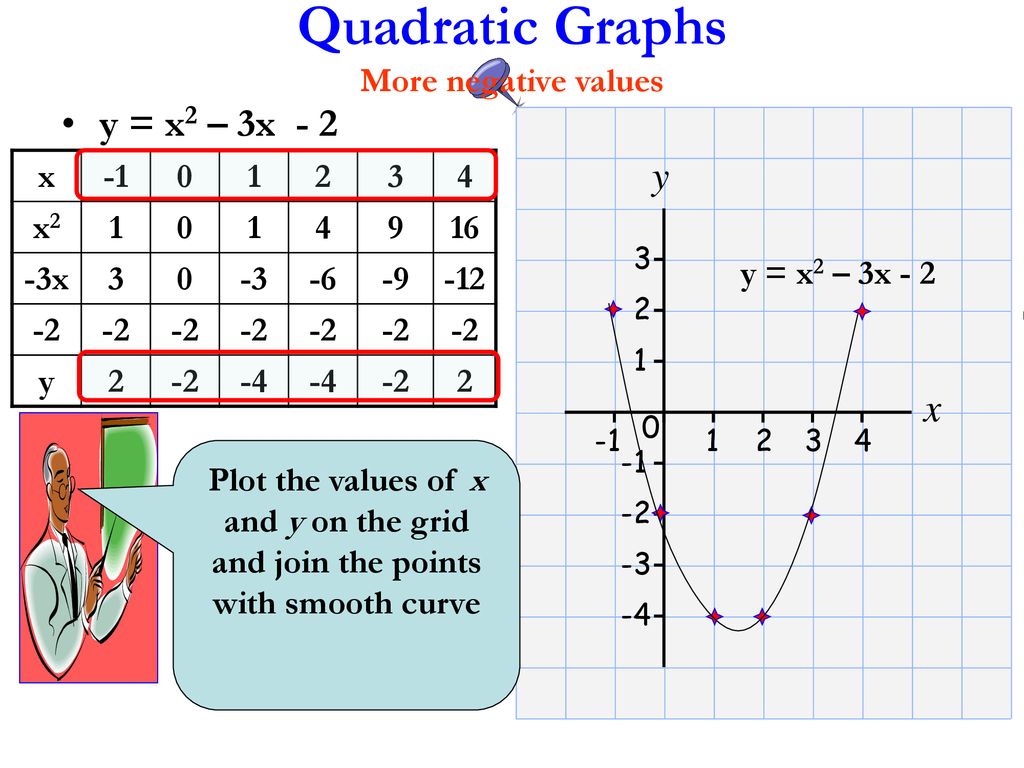
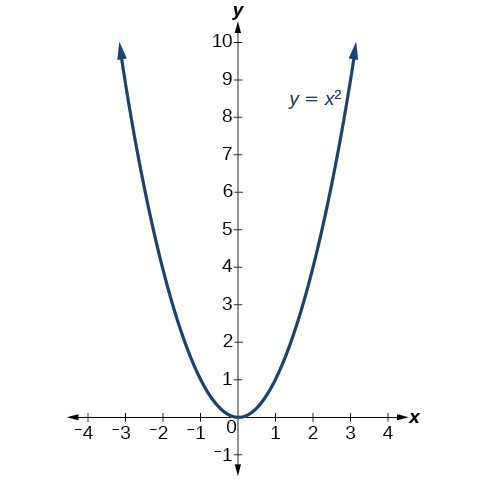
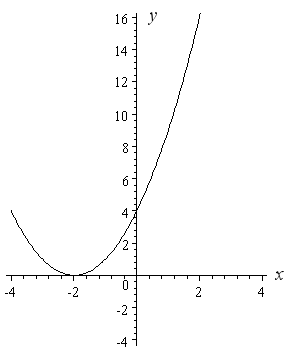
ContourPlotx^2 y^2 == 1, {x, 5, 5}, {y, 5, 5}, Axes > True, Frame > False, AxesLabel > {x, y} Share Improve this answer Follow answered Nov 29 '15 at 657 user9660 user9660 $\endgroup$ Add a comment 2 $\begingroup$ Taking Rahul's idea ContourPlot3Dx^2 y^2 == 1, {x, 2, 2}, {y, 2, 2}, {z, 2, 2} Share Improve this answer Follow answered Nov 29 x / y y / x > 2 Erweitern, auf einen Nenner bringen x^2 /( xy) y^2 / (xy) > 2 ( x^2 y^2 ) / ( x * y ) > 2 Im Zähler steht immer etwas positives Im Nenner steht bei einer positiven und einer negativen Variablen etwas negatives, also ist der ganze Bruch negativ und somit < 0 mfg Georg Beantwortet von georgborn 114 k 🚀 Ein anderes Problem?Y = x 2 2 is a quadratic equation of the form y = ax 2 bx c, let a = 1, b = 0 and c = 2 You can certainly plot the graph by using values of x from 2 to 2 but I want to show you another way I expect that you know the graph of y = x 2 If you compare the functions y = x 2 and y = x 2 2, call them (1) and (2), the difference is that in (2) for each value of x the corresponding value
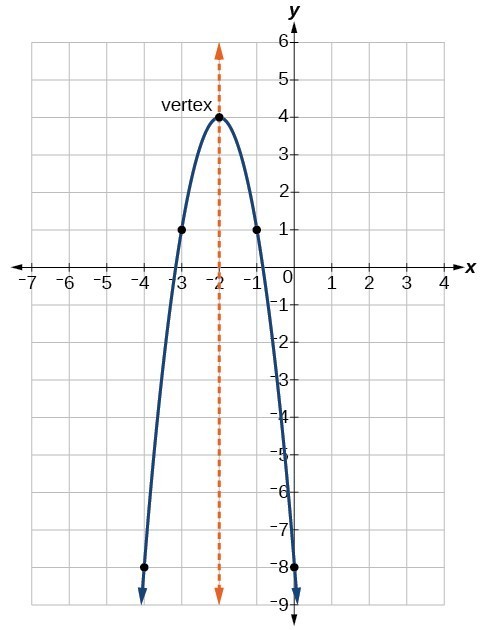
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyDirection Opens Down Vertex (−1 2, 9 4) ( 1 2, 9 4) Focus (−1 2,2) ( 1 2, 2) Axis of Symmetry x = −1 2 x = 1 2 Directrix y = 5 2 y = 5 2 Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex2 Aufgabe (a) DefiniereA n= f(x;y) 2R2 jx2y2
Y x 2 2 m-1 x 3-m 2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
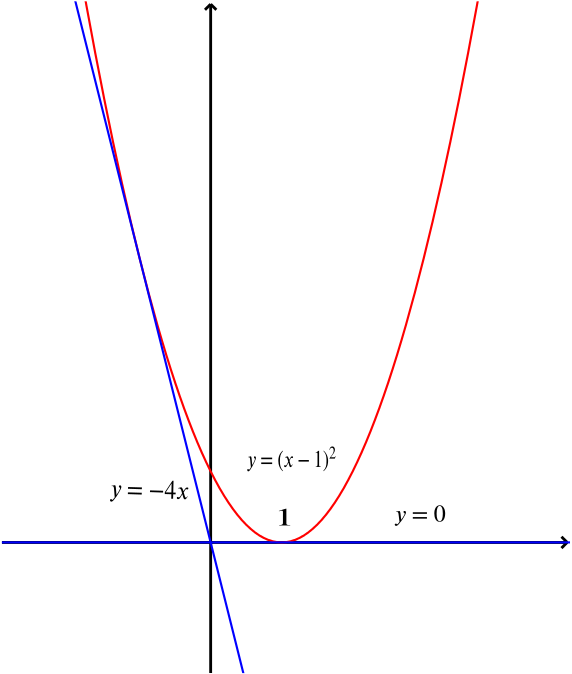 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | 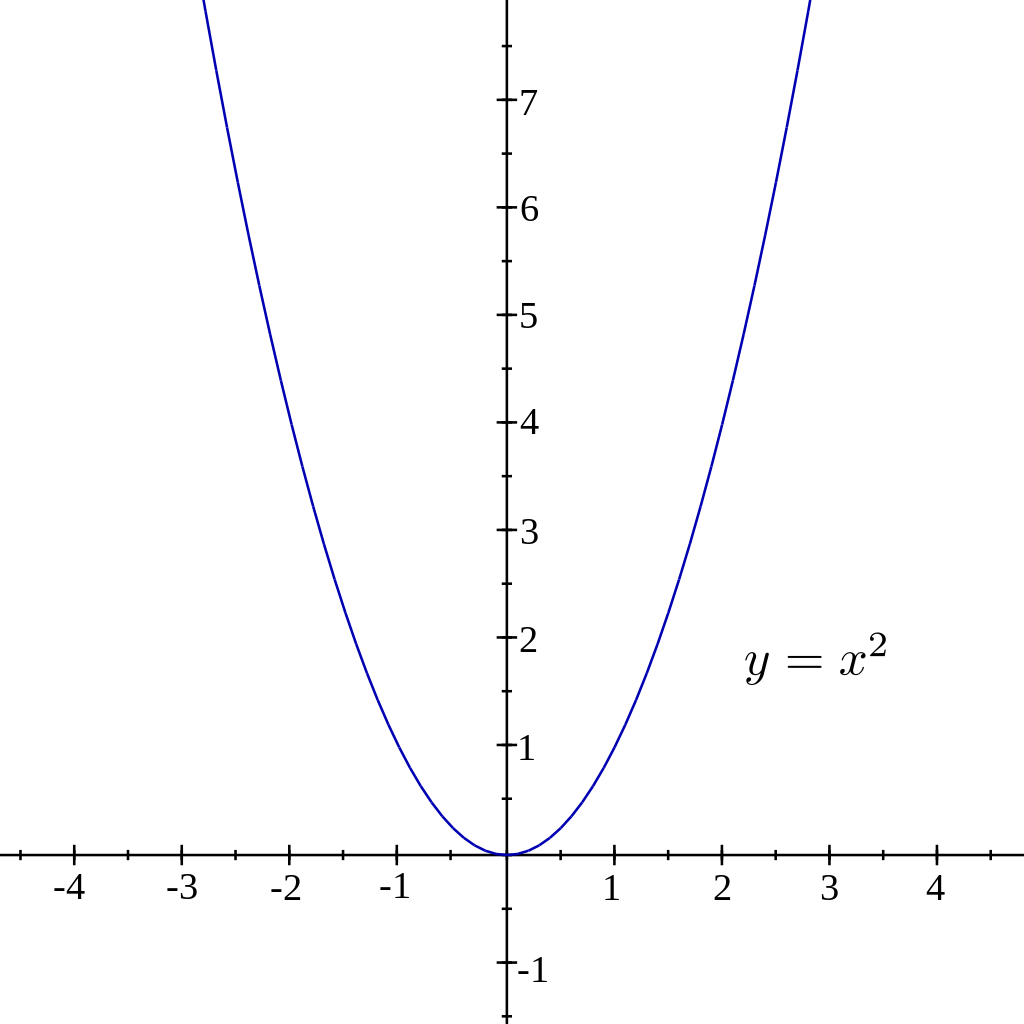 Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions | 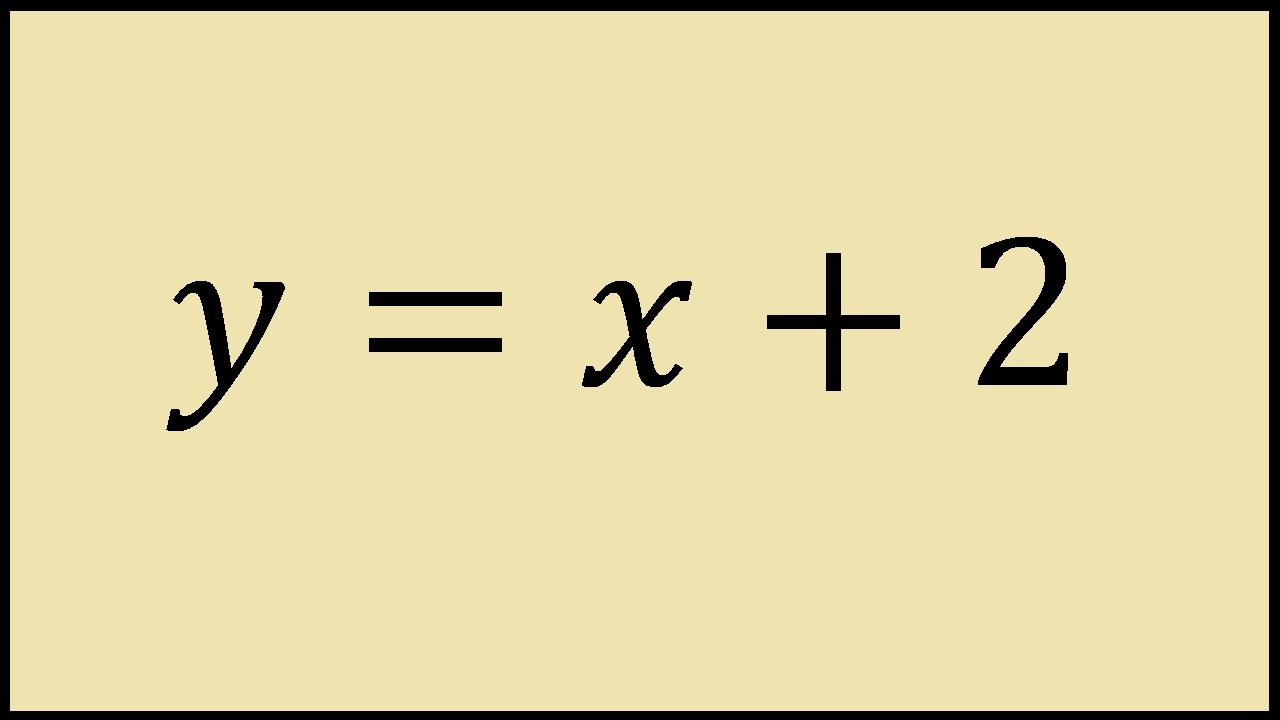 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | 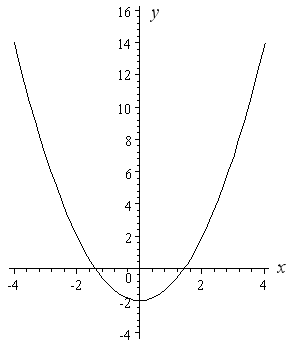 Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | 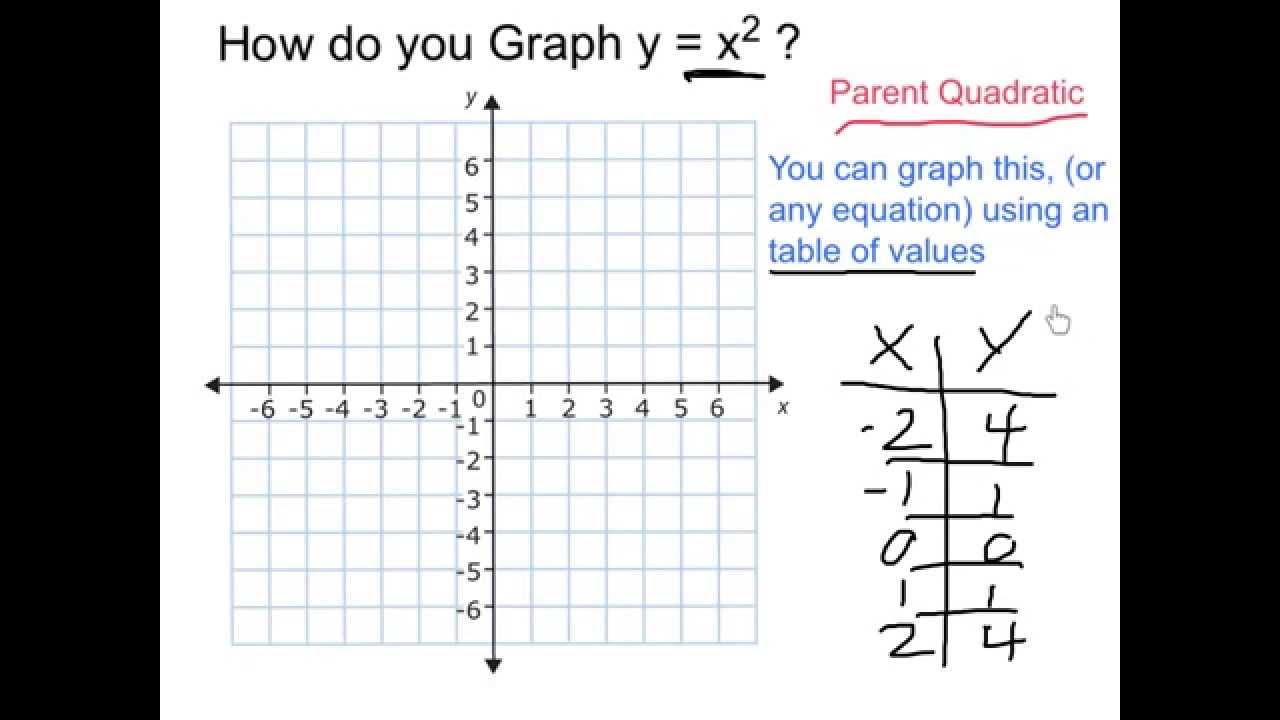 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | 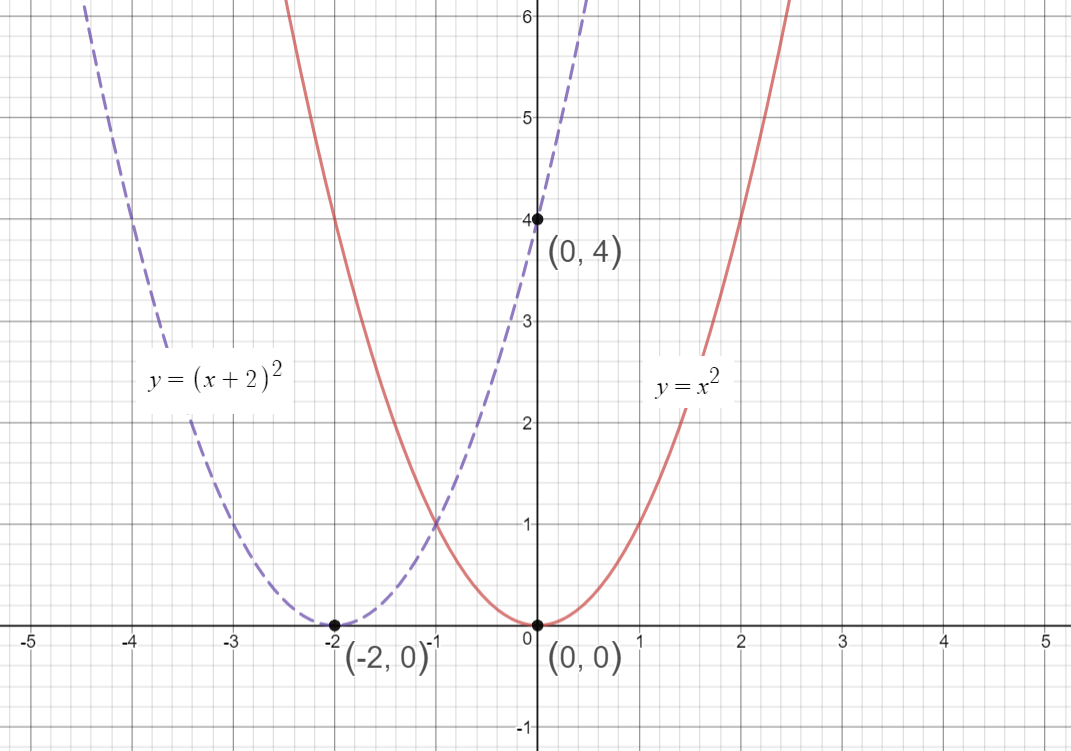 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | 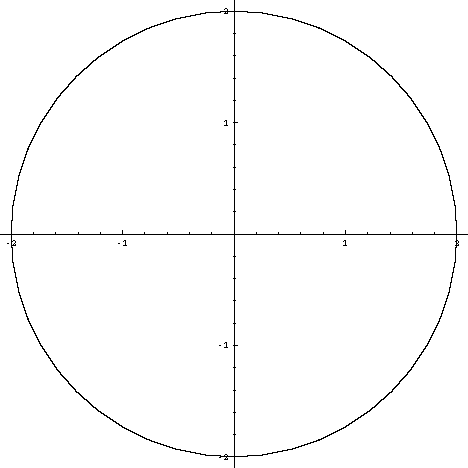 Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions | Graph Domain And Range Of Absolute Value Functions |
 Graph Domain And Range Of Absolute Value Functions |  Graph Domain And Range Of Absolute Value Functions |
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel2x2y(x2 y2) 2x2y3 (x2 y2)2 = 40 2x4y (x2 y2)2 = 0 folgen nur die l osungen x= 0, ybeliebig T= 10, ybeliebig ;y= 0 T= 10 Die erste dieser l osungen ist die Gleichung des linken Randes, die zweite L osung ist die Gerade, die den Halbkreis in zwei Viertelkreise teilt Da f ur die Temperatur T 10 gilt, handelt es sich in beiden F allen um Maxima Nun betrachten wir die Temperatur an den
Incoming Term: y x 2 2, y x 2 25/x, y x 2 2x 1, y x 2 2x 3, y x 2 2x 24, y x 2 2/x 2-4, y x 2 2xy-y 2, y x 2 2- x-1 2, y x 2 2y+6 2 x+3, y x 2 29x-29 e 2-x, y x 2 25 x 2-x 3/x, y x 2 2y 6 2 x 3, y x 2 2 m 3 x 3-m, y x 2 2 m-1 x 3-m 2, y x 2 2 t-1 x-4t 5, y x 2 2 2 x 4 4 4,
コメント
コメントを投稿